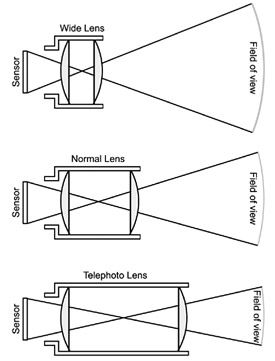
Fig. 1
LOS ANGELES
In the world of digital video, there is much ado about depth of field, and deservedly so. Decreased depth of field is one of the more attractive attributes of the "film look." However, many digital video shooters don't have a firm grasp on field of view. Whereas depth of field denotes the area before and after the plane of focus that will appear in an acceptable range of sharpness, field of view denotes the total area (both horizontally and vertically) that will be captured by a given lens onto a given target (Fig. 1).
FOCAL LENGTH
The basic properties of a lens are to capture the light from a given field of view and project that light onto a given target size. With today's extraordinary selec-tion of sensor sizes (1/4", 1/3", 1/2", 2/3", Super 35, full-frame still camera, etc), many people are turning to smaller, more inexpensive sensor sizes and then util-izing higher-quality lenses intended for larger formats. This often yields an improvement in the quality, sharpness and contrast of the image, but also alters the respective focal length of the repurposed lens.
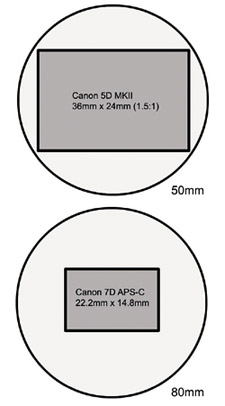
Fig. 2 One of the hot topics in the HD world is the Canon EOS 5D Mark II hybrid DSLR (digital single lens reflex) still and HD camera. The camera features a CMOS sen-sor the size of a traditional 35mm still frame at 36mm x 24mm large. Compared to the standard Super 35 motion picture frame size (24.89mm x 18.76mm), the CMOS sensor is nearly twice the size of the film frame. This means that lenses designed for the 5D camera have to project their image onto this large area.
Lenses, which are circular, project a circular image, not a rectangular one. So every lens has a certain amount of image that is "wasted" because the target (sensor or film frame) is only "seeing" a rectangular portion of that projected circular image, (Fig. 2). Lenses designed for a particular format are optimized to project their sphere to evenly cover the actual rectangular target size with little waste.
If we take a 50mm lens designed to work with the full-frame 35mm still camera, like the 5D Mk II, and use it on a Canon EOS 7D, which has a "crop" (smaller) sensor that is 22.2mm x 14.8mm (slightly smaller than the standard Super35mm film frame), the lens is projecting it's image over a considerably larger area than the actual physical size of the sensor. As a result, we have a lot more wasted image because the sensor only "sees" a fractional portion of the lens image.
RESEARCH & GEOMETRY
This alters the field of view of the lens and, alters the apparent focal length. What was, originally, a 50mm lens on the 5D Mk II, is now the equivalent of an 80mm lens on the 7D.
The smaller the sensor size, the longer the apparent focal length of any given lens. Fig. 3 shows an approximation of using a 5D Mk II 50mm, from the same physi-cal distance to the subject, on several smaller sensor cameras. This is not to imply that the 5D lenses should (or can) be used any camera, it's merely an example of how apparent focal length is changed by changing the sensor size.
Fig. 3: Fields of view of a given subject as seen by a 50mm lens and various sensors. Determining what apparent focal length you will be seeing from any given lens from another format requires a little research and some geometry.
First, you need to know the actual physical dimensions of the sensors in each of the cameras—the larger format you're borrowing a lens from and the smaller format you'll be using it on. Not all manufacturers readily provide this information, but this is the age of the Internet, and with some digging you can find the info you're looking for.
If we're working with a lens made for the Canon 5D Mk II, with a sensor size of 36mm x 24mm, on a Canon EOS 7D, with a sensor size of 22.2mm x 14.8mm, we need to find out the lens equivalency factor. In order to do that, we need to find the diagonal measurements of each of the sensors.
Fig. 4: Understanding sensor size is as simple as A2 + B2 = C2 This requires cracking out a little high school geometry and Pythagorean theorem to find the hypotenuse of a right triangle: A² + B² = C² (Fig. 4). A and B repre-sent the length and width of the chip, so for the 7D we have 362 + 242 = C² (C= diagonal). 1296 + 576 = 1872. Then figure out the square root of 1872 and you get a diagonal of 43.27mm. For the 7D, we find 492.84mm + 219.04mm = 711.88mm—find the square root and we have 26.68mm diagonal. Divide the larger diagonal by the smaller and we get a factor of 1.62x.
So a lens from a 5D Mk II on a 7D will have an apparent focal length of 1.62x longer. A 50mm becomes an 81mm. A 10mm becomes a 16mm and so forth.
These calculations were of paramount importance to cinematographers who first made the leap from film to digital with 2/3" cameras. Understanding the 2.5x lens factor was important in making lens selections and becoming comfortable with the new medium. They're also important when utilizing lens adapters like the JVC CA13U, which does not feature an intermediate ground glass to refocus the image.
Jay Holben is a director, producer and cinematographer working in Los Angeles, He is also the Technical Editor of DV magazine.
