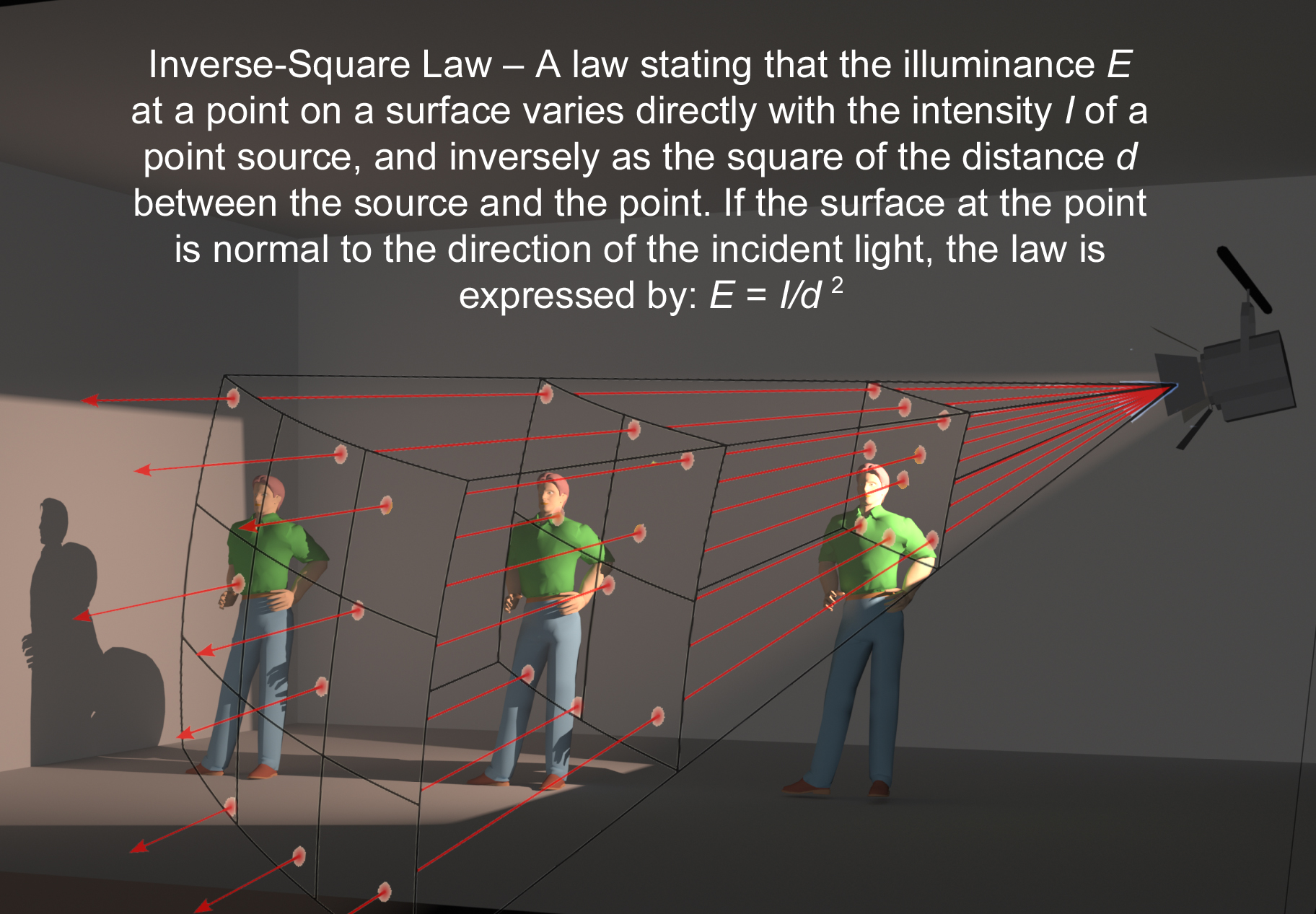
Anyone who’s delved into lighting knows that it’s a complex blend of art, craft and science. Within that pillar of science is the formula, which helps us predict how lights spread over distance—The Inverse-Square Law.
Fortunately, you don’t need to be a physicist to understand this little bit of energy propagation science. This subject is usually presented as a formula to solve, but my goal is to cover it in a way that even math-phobic people, like myself, can understand. Here’s the sum of it.
The Inverse-Square Law describes how point-source light spreads out over an area. Intensity is inversely proportional to the square of the distance between light source and the measuring point. Got that? If not, relax.
I’m going to be a bit heretical here and save you the pain of memorizing a math formula that you’ll probably never calculate. Those who run this computation are more likely to be engineers involved with the I.E.S. (Illuminating Engineering Society) than I.A.T.S.E. (International Alliance of Theatrical Stage Employees). For the rest of us lighting folk, I offer you a rule of thumb that I hope you’ll find more accessible:
- Reducing the distance to a light by one-fourth doubles the brightness.
- Increasing the distance from a light by one-fourth halves the brightness.
The closer the light is to your subject, the more drastic the change of intensity for any variation in distance. This is particularly relevant today, as many LED fixtures are frequently used relatively close.
Another reason not to worry much about the precise calculation of Inverse-Square is because it’s based on a “point source.” That requires the distance from the lamp to measuring point to be at least five times the width of the light emitting aperture. Given the larger aperture size of many LED fixtures today (such as panels and tubes), a lot of fixtures don’t fit the “point source” description at the distance they’re used.
Precise point-source calculations simply aren’t useful in predicting the light drop-off of large aperture sources. Intensity still changes over distance, but not in the manner that the Inverse-Square Law promises. If we’re interested in the practical application of light, we must accept that reality beats theory every time. Fortunately, there are lighting techniques designed to smooth the intensity that don’t require advanced math skills.
Let’s look at an example where a point-source light is relatively close to the subject. In this case, our subject is 6 feet from the light, and the intensity measures 100 foot-candles. Moving the subject just 18 inches towards the light (which is ¼ the total distance) doubles the brightness to 200 fc.
This drastic change works in both directions. Moving the subject away from the light by the same 18 inches will halve the intensity to 50 fc. Those changes are huge from the standpoint of camera exposure. One short step in either direction would result in being over-exposed, or underexposed, by a full f stop. Fortunately, there are practical techniques to minimize this impact.
Making Artificial Light More Natural
Our goal in covering this isn’t just about sidestepping the Inverse-Square Law. Minimizing the impact of abrupt-intensity-change benefits more than just minimizing exposure swings. Lighting that’s consistent across a broad area appears more natural.
As in most things, nature is the best teacher. Our most fundamental light source is the sun. At its relatively infinite distance from the Earth, its rays are parallel. Collimated rays aren’t impacted in a meaningful way by The Inverse-Square Law. The sun is a prime example of how great distances between the light source and the subject minimize intensity changes. By the time sunlight enters our neighborhood, the intensity will be the same all along its path.
Light in the real world tends to vary brightness more subtly than our added production lighting. Practical lamps cast their light in accord with our expectations of the real world. If you want your reel world to look like the real world, your lighting would do well to follow nature.
The way you create your lighting should be invisible to the audience. In support of that goal, masking the impact of the Inverse-Square Law is akin to smoothing the brush strokes of a painting. If your aim is realism, let your audience be free to concentrate on what you’ve painted, rather than how you’ve painted it.
Tips on How to Finagle the Inverse-Square Law
Distance: The primary technique to mitigate abrupt intensity change is to work the lights from farther away. This approach requires more output from your lights to deliver the desired intensity from a greater distance. Higher-output fixtures, with excellent color fidelity, are always a good choice. It’s better to dim down a powerful light fixture than have to move an under-powered one closer. Avoid close-in fixtures whenever possible.
Modifiers: Another means to finagle the Inverse-Square Law is to change the intensity by intervening along the path of the light. Light is malleable. Shaping and shading light can be done with a variety of modifiers. Scrims, flags, nets, reflectors and diffusers can be inserted into the light path to manipulate both the quantity and quality of the light.
One common technique to “cheat” the Inverse-Square Law with a Fresnel is to place a half-double scrim in the accessory slot. The scrim can be positioned to hold back whichever part of the beam would otherwise be too bright for the nearby subject. This is especially useful in smoothing the intensity whenever talent moves toward a light.
Nets, diffusion filters and flags are some of the different modifiers that can be placed in the beam to selectively reduce parts of the total area. Whether clipped to the barn doors or held more precisely by C-Stands and gobo arms along the path, these modifiers can attenuate selected portions of the beam to smooth intensity.
On some beam fixtures, you can use the less-intense outer edge of the light (the “field angle,” as opposed to the central “beam angle”) to smooth and blend the light levels. Likewise, soft-lights and LED panels with “control screens” or “egg-crate” louvers may be panned or tilted slightly off the main focus to provide a less-intense light from the edges of the light.
One novel approach to minimize the impact of the Inverse-Square Law uses mirrors and assorted reflectors to increase the total throw length of the beam’s path. This effectively folds the light to increase the light-to-subject distance. This unconventional technique has been well-demonstrated by Cinematographers Dedo Weigert and Christian Berger to excellent effect.
Even though physics dictates the behavior of light, we have the tools and techniques to sidestep those limits to better serve our purpose. Inverse-Square turns out to be more of a suggestion than an unbreakable law.
