The Inverse Square Law of Illumination has been with us for so long and is commonly taken for granted that it might seem to be a questionable subject for discussion. I feel revival of interest in this deep-rooted rule is justifiable due to surprising results observed in a recent set of tests.
THE BASICS
The Inverse Square Law clearly states that it is applicable only in the case of a point source of light. We usually don’t use point sources directly, just as part of an instrument. Typical practical point sources of a small size would be short arc discharge lamps as well as compact tungsten filaments.
A corollary that is always added to the Inverse Square Law is that for the purpose of estimating illuminance (foot-candles or lux), a source is assumed to be a point source if the distance from the source to the illumination plane is at least five times the widest dimension of the source. Some more conservative illumination experts say this distance should be greater than 10 times. For example, to be able to use the law for a 6-inch Fresnel spotlight and taking the more cautious approach, the distance from the fixture to the light meter must be greater than 30 inches. Therefore, if I measure 600 foot-candles at 5 feet from my spotlight, the Inverse Square Law says I should measure 150 foot-candles at 10 feet:
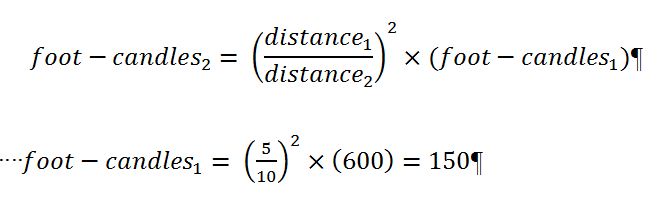
Very straight forward.
THE QUESTION
While gathering data for my article on the Shadow Factor (Lighting Technology, Nov. 7, 2012), it seemed an ideal time to determine the answer to a question I had always wondered about. If the Inverse Square Law should not be applied at distances closer than, say, 10 times the maximum size of the source, what is the relationship between the measurement distance and the incident light at points close to source, within the 10 times limit? Could it perhaps magically approach a linear relationship? I must warn the reader at this point that the results I obtained were, disappointedly, not as neat and orderly as a “law” should dictate.
THE METHOD
To attempt to answer my question, I used a conventional 4kW Super Softlite for the test. The aperture of the fixture is 30-by-36 inches, a relatively large source. I measured the foot-candles at the center of the beam of the instrument every 2 feet from the front of the fixture from two to 49 feet. Then I plotted the data on a log/log scale graph.
First, I chose to plot distances greater than 10 times the instrument’s width in order to be as conservative as possible, in other words, distances greater than 30 feet (10 times the 3-foot width of the Softlite). The resultant curve was, happily, a straight line when plotted in the log/log scale indicating that a simple power function of the form: y=kxb could describe the curve (k being a constant). If the Square Law is, in truth, a law, the value of b, the exponent should be –2 in this case as the measuring distance is greater than 10 times the fixture’s aperture.
Disappointingly, when I applied the curve fitting ability of my spread sheet application, I came out with an exponent of –1.828, close, but not –2.000. This is shown in Fig. 1. I have included an idealized plot (in red) that shows what the curve would look like if the Square Law represented the data.
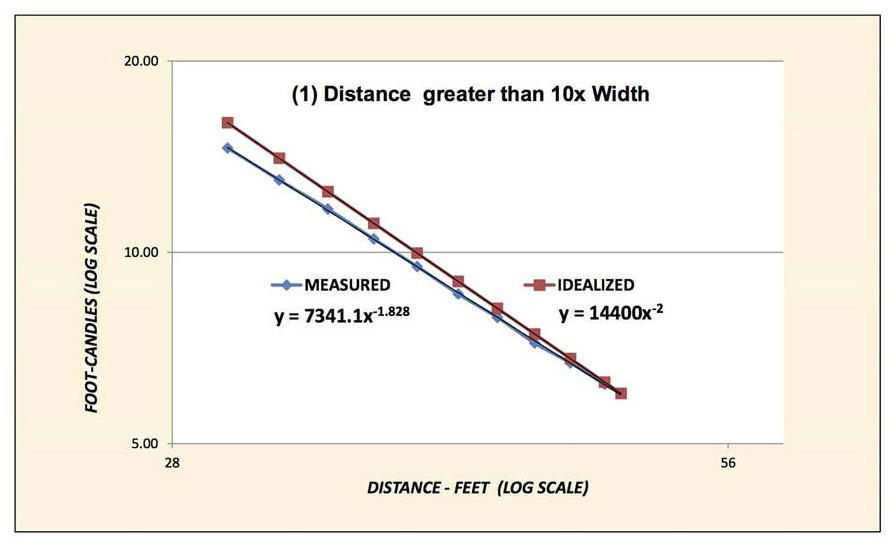
Fig. 1: Distance greater than 10 times the widthCHECKS AND BALANCES
At this point, I thought that I’d better check to see if I could find any published photometric data for similar large sources to compare. What I found was interesting.
One reputable company just gave a figure for candlepower and two values for illuminance at selected distances; the illuminance was obviously calculated from the candlepower listed using the Inverse Square Law. I think this was in order to simplify the data, as the casual user might only be interested in the order of magnitude of the illuminance rather than a value carried out to 10 places.
The manufacturer’s data for the Softlite I used did not have as many measurement distances as were in my test, but I was relieved to see that that data did not obey the Square Law as well. The exponent was –1.919, compared to –1.954 that I calculated for similar range of distances with my data. I could only find one other set of data for a large source. These readings were extensive except that they were only in range of less than 10 times the width, in other words where the Inverse Square Law should not be applied and revealed an exponent of –1.869, which I felt gave some credibility to the data I acquired.
THE ANSWER
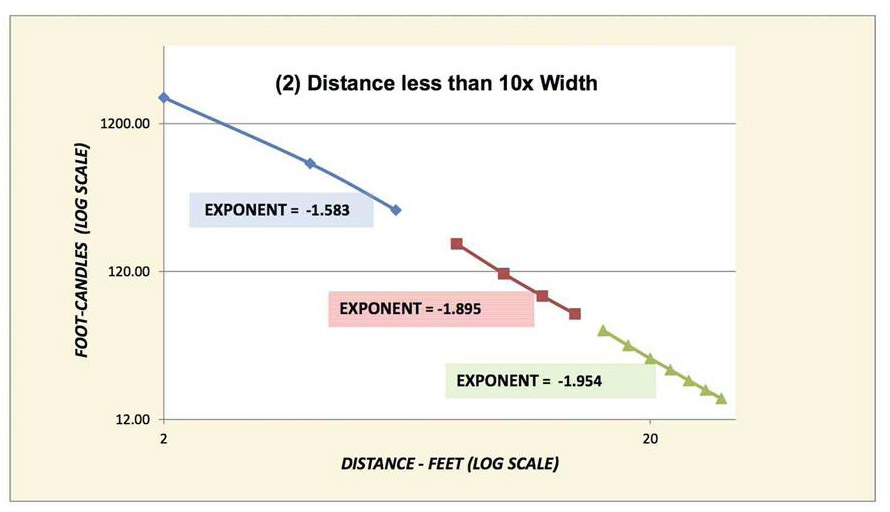
Fig. 2: Distance less than 10 times the width Let’s go back to the original problem of what function could define the illuminance where we are in the unacceptable distance range. Referring to Fig. 2, I have split my measurements into three sections in order to see if a trend exists. Success at last.
You will notice that the exponent of the function decreases from the nominal theoretical value of –2.0 as we measure closer to the lamp. In my case the three ranges gave exponents of decreasing values as the distance decreases from –1.954 to –1.895 and finally, –1.583. [I would guess that the exponent might actually be –1.0 at some point very close, perhaps a millimeter or so, from the fixture.]
As a result of my efforts, I think I can safely make the following statements with some degree of conviction: 1) The Inverse Square Law can be used be to approximate illuminance at other distances where illuminance is known at one distance, if all distances are greater than 10 times the source’s maximum dimension; 2) Where the distances are less than 10 times the large source’s maximum dimension, the Inverse Square Law does not apply precisely, but can be used to yield a useful guess. Not too scientific, but no one said lighting is a science.
Bill Klages would like to extend an invitation to all the lighting people out there to give him your thoughts atbillklages@roadrunner.com
