‘But It Sounds the Same’: Why Audio Measurements Differ

Dave
Moulton
You may recall that we’ve been grappling with the measurement of audio loudness and the implications of the ITU’s B.S. 1770-1 standard for the measurement of loudness, in support of the CALM Act.
I promised we would consider the effect of this standard on the audio levels we measure. Just so you know, this is background information to add to your understanding of a difficult topic. You don’t have to do anything with this, except try to understand it, sort of. Thanks.
THE NATURE OF WEIGHTING CURVES
Approximately 80 years ago, Harvey Fletcher and Wilden Munson determined, through measurement, that the frequency response of human hearing varies as a function of loudness change.
This led to their creation of a set of so called “Equal Loudness Contours,” which show the inverse of the frequency response of human hearing over the range of levels that humans hear comfortably, in 10-decibel increments (anchored at 1 kHz. and called “Phon” curves).
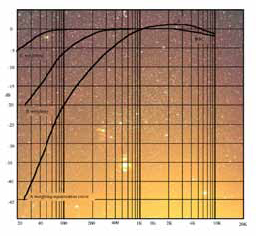
Fig. 1: A-, B- and C-weighting curves, using a logarithmic scale (from “Total Recording”)
These Equal Loudness Contours are of profound importance to us in audio and acoustics. However, they are too complex (as a data set), for easy use in measuring human hearing or in measuring the effects of various signals at various levels on human hearing. As a result, simplified “weighting” curves were derived from these contours, to be applied in Sound Level Meters. The primary curves are A-, B- and C-weighting.
In a simplistic, but reasonably useful way, you can think of A-weighting as derived from the 40 Phon Equal Loudness Contour (derived from how we humans hear at a level of approximately 40 dB Sound Level, which is quite soft); while B-weighting is approximately appropriate for the 70 Phon Contour (70 dB Sound Level, a medium loud level for us); and Cweighting is useful for measuring how humans hear at around 100 dB Sound Level, which is loud for us.
The professional video industry's #1 source for news, trends and product and tech information. Sign up below.
Fig. 1 shows the A-, B- and C-weighting curves. These can be thought of as equalization curves applied to the signal just before it is measured (but not in the signal path to the loudspeakers!), so that the measurement approximates the spectrum perceived by humans at soft, medium or loud levels.
HOW WEIGHTING CURVES AFFECT SIGNAL MEASUREMENT
Naturally, when we apply such equalization to a signal, it affects the overall level of the signal as well as its spectrum. In the case of A-weighting, for instance, the bottom octave of the spectrum (31 Hz.) is attenuated by 33 dB, the second octave (63 Hz.) by 21 dB and the third octave (125 Hz.) by 11 dB.
This means, for instance, that energy in these octaves is essentially not included in the level measurement of the signal. If that part of the audio spectrum contains significant energy, then the overall energy measured will be less than it would be with a so-called “broad-band” measurement.
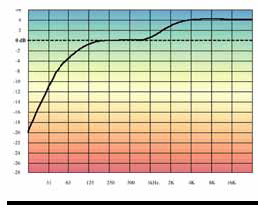
Fig. 3 shows the approximate difference in Leq level for each weighting and excerpt, compared to broadband measurements.
So, weighted measurements can be a little tricky. Weighting doesn’t just “correct for how humans hear,” but it also can change the indicated level, often by quite a bit. Unfortunately, the amount of change depends on the nature of the signal, as well as the type of weighting.
In the case of B.S. 1770, the B-weighting curve is modified (actually lowered somewhat in frequency, letting more upper bass be measured), and then the entire spectrum from 2 kHz. on up is boosted by 4 dB.
The resulting curve is called “K-weighting,” and it is the weighting that B.S. 1770-1 requires us to use for determining loudness. Fig. 2 shows K-weighting across the 10 octaves of the audio spectrum.
USING DIFFERENT WEIGHTING SCHEMES
To give you an idea of the effect of these weightings, I made audio level measurements of six different audio signals: a Sine Wave at 1 kHz.; Pink Noise; an excerpt of a woman reading text; a solo classical piano excerpt; a bluesy Mark Knopfler excerpt; and a loud arena-rock excerpt.
After making broadband measurements of Leq for each of these excerpts, I then measured them again with A-, B-, C- and Kweighting. The table in Fig. 3 shows the approximate difference in Leq level for each weighting and each excerpt, compared to the broadband measurements.
Note that with a 1 kHz. sine wave, all the weightings are pretty much the same (except for the slight boost due to the highfrequency shelf in K-weighting). For Pink Noise, K-weighting increases the measured level by a dB, while the other weightings reduce it by up to 3 dB.
The spoken voice loses almost 4 dB in level when A-weighted, but otherwise is pretty much unaffected. The effect on this particular classical piano excerpt is similar. The blues ballad excerpt has a pronounced bass track, leading to real measurement variations with all but Cweighting.
The arena rock excerpt has lesser variations. Note that C-weighting is pretty benign in this regard, and doesn’t affect any of the signals except Pink Noise very much.
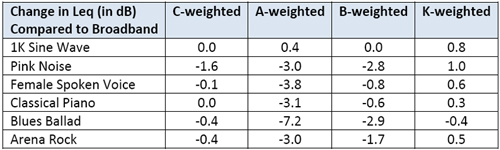
Fig. 2: K-weighted response, based on a revised B-weighting curve with a 4 dB high-frequency shelf boost added. Shown using an octave band scale. In the case of K-weighting—our real object of interest here—the level drop from the revised B-weighting is often offset by the increase in high-frequency energy. In effect, the spectrum is being tilted for measurement, so level losses at low frequencies are “made up” at high frequencies for broadband signals.
WHAT IT ALL DOES AND DOESN’T MEAN
There are several insights to be gained from this. First, there is no such thing as unequivocal audio level or loudness. Second, as a matter of course, this is quite fuzzy data and it varies as a function of time, spectrum and weighting. Third, variations of a dB or less are pretty much insignificant.
Finally, bass is really a wild card here and can result in big level misreadings. (I generally expect to find dBA noise pollution measurements to be 6–8 dB softer than broadband measurements of the same sound.)
Fortunately for you, K-weighting does not generally change level very much. Be aware, however, that you can inadvertently drive K-weighted readings up with too much dialog or other high-frequency content in your mix, because of that spectrum tilt.
One final bit of advice: don’t obsess about this. I share it with you so you can know a little more about what is actually going on in this very difficult aspect of audio.
Keep this information in your hip pocket for reference, but don’t drive yourself into a froth of anxiety and control freakdom trying to resolve the last .2 variation in dBA, or is it dBK? Thanks for listening.
Dave Moulton keeps waiting for his weighting to go down. Keep in mind, you can still complain to him about almost anything at his website,www.moultonlabs.com.

