Our CALM story so far…
Last month, I promised to discuss with you the audio measurement protocol known as B.S. 1770-1 (from the ITU), pursuant to a discussion of measured broadcast playback levels that I made and reported on earlier. B.S. 1770-1 is a protocol (an algorithm, actually) for modifying the television audio signal to measure its magnitude in a way that more closely agrees with humans' subjective sense of loudness. The protocol also includes another feature having to do with the detection of digital peaks, which we are not going to discuss here.
B.S. 1770-1 is now mandated, through the CALM Act, as the approved way to determine the broadcast level of an audio signal (mono, stereo or multichannel). That level is expressed as "Loudness" (more about that in a moment), and is referenced to Full Scale of a digital audio signal, and is more formally known as "LKFS" (L stands for Loudness, K for the spectrum weighting of the signal to be measured, and FS stands for Full Scale, of course). A change of 1 LKFS is the same as 1 decibel (ca. 12 percent change in amplitude).
What this means is that, if you intend to comply with the CALM Act, you need to use a (digital) audio meter that contains the B.S. 1770-1 algorithm and applies it to the signals to be measured.
LOUDNESS VS. AMPLITUDE OR SUBJECTIVE VS. OBJECTIVE
As an acoustician working mainly on psychoacoustic issues, I have my quibbles about this. From my standpoint, loudness is a subjective sensation, not a physical quantity. Objective Loudness is an oxymoron in my world—there's actually no such thing, got it?
Well, now, set it aside. For your purposes, my psychoacoustic quibbles are irrelevant. The reality is that the frequency response (K-weighting) applied to the audio signals as a function of measuring them comes from a well-researched, good-faith and highly relevant effort to improve the correlation between our subjective sense of loudness and objective physical changes in amplitude.
As you probably know, the frequency response of our hearing is not "flat," nor is it linear or constant; it changes dramatically as a function of level. Finally, hearing is variable from listener to listener. So, whatever effort we make to approximate a typical "human" hearing response needs to aim for a "probable range of responses" under a "probable range of conditions" and then accept that the result will be quite "fuzzy" in terms of accuracy. I personally think that the response curves at the heart of the B.S. 1770-1 algorithm do quite a good job at this.
The net result is a correction that yields "loudness approximations" that are going to be pretty reliable for most of us couch potatoes when we are curled up on our reclining sofas with our big-screen LCD monitor and 5.1 audio system, soaking up our cultural heartland. Let's talk about what, specifically, is being done to make amplitude more closely resemble loudness.
THE PROTOCOL
As already noted, our hearing is not flat; we have a pronounced rise in our hearing sensitivity, peaking around 4 kHz and almost two octaves wide (it varies with the amplitude of the sound), (see Fig. 1). To approximate that rise, the algorithm uses a high-frequency shelf that hinges at about 1 kHz and boosts the entire spectrum above 3 kHz by about 4 dB, (see Fig. 2).
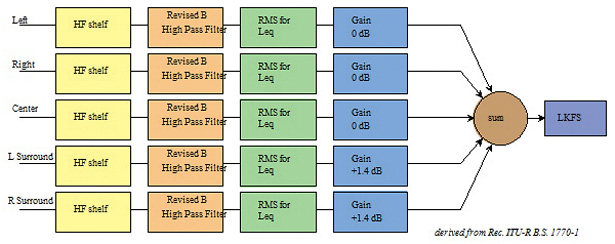
Fig. 1: Flow chart of the B.S. 1770-1 algorithm used to determine LKFS
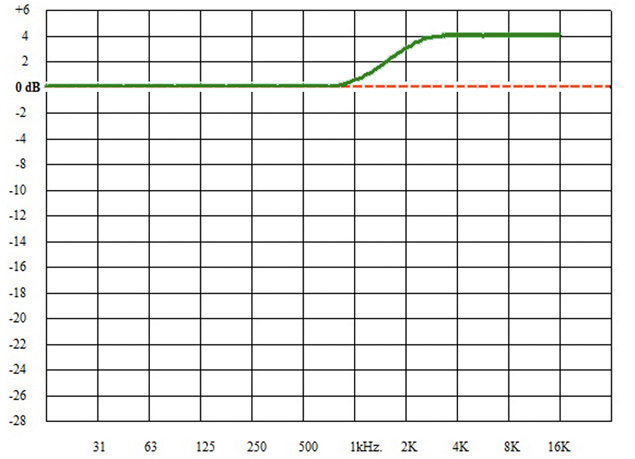
Fig. 2: Flow chart of the B.S. 1770-1 algorithm used to determine LKFS After that, the algorithm uses a modified version of the B-weighting curve, (see Fig. 3). B-weighting is intended to approximate human hearing at moderately loud levels (it is, I think, modeled roughly on the inverse of the 70 Phon Equal Loudness Contour, which is anchored to 70 dB SPL at 1 kHz.). In any case, the revised B-weighting filter used for B.S. 1770-1 begins to roll off below 200 Hz, and is down ca. 15 dB at 20 Hz, (see Fig. 4).
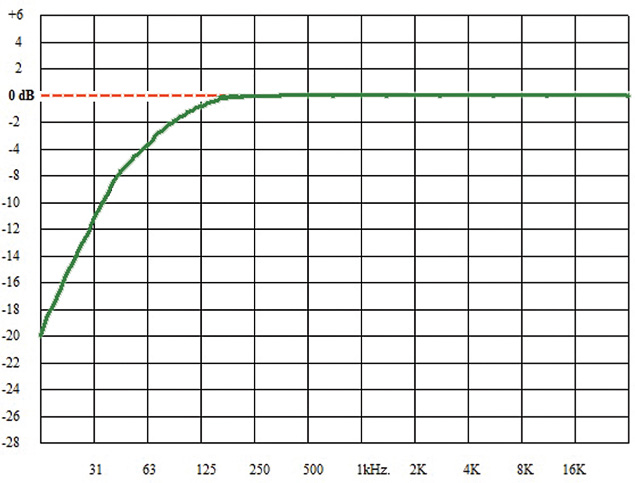
Fig. 3: An approximate response curve of the revised B-weighting high-pass filter used in the B.S. 1770-1 algorithm
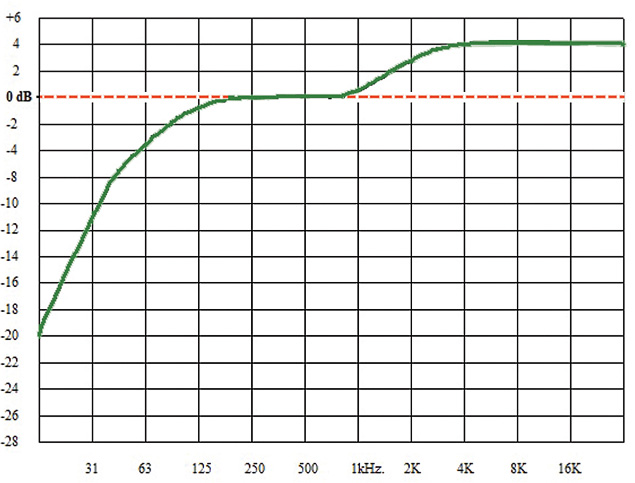
Fig. 4: The resulting approximate composite K-weighted response curve used in the B.S. 1770-1 algorithm After these filters have been applied, the Leq (or average relative power over time) of each channel's signal is taken. Gain is then applied for the surround channels (+1.4 dB) and then all the Leq values are summed to create the so-called LKFS level. This is the level you need to use when determining if you are in compliance with the CALM Act. How you use that level depends on your particular role in the creation or transmission of that broadcast signal (see the ATSC Recommended Practice A/85).
WHAT IT ALL MEANS
The theory (which I think works pretty well here) is that when such a response curve such as K-weighting is applied, the resulting changes in program level adhere more closely to subjective human estimations of changes in loudness than does simple amplitude change. As a result, such levels can be used successfully to estimate relative "loudnesses" of different programs for a wide range of end-listeners.
This means that, if we use these measured levels (which we call "loudness" even though they aren't) carefully, we should have more uniform and predictable loudnesses for our end-users.
And that is why Patrick Waddell at Harmonic is correct when he says that measurements of audio levels for television broadcast should be compliant with the standards of B.S. 1770-1.
A couple of other things to note: first, the LKFS level is a monaural sum of however many channels are in use in any given case, so complex multichannel mixes will tend to be louder than mono signals for any given observed channel level; and, second, the LFE channel is not included in the loudness estimation, which I personally think is the correct thing to do, simply because its result is so widely and wildly variable (and unpredictable!) in end-user situations.
Next month, I will show you the measured effect of A, B, C and K-weighting on the amplitudes of a variety of broadcast signals, just so you have an idea what these relationships are.
Thanks for listening.
Dave Moulton is busy dealing with spring, allergies and other trivial pursuits. However, if you can wake him up from his afternoon nap you can complain to him about almost anything at his website, moultonlabs.com. He really does try to be a good listener!
