Alert readers may recall that I discussed subwoofers in the July 6 issue of TV Technology.
Well, Bob Dixon, director of Sound Design for the NBC Olympics) wrote to ask if I would go a bit further with this. He wrote: "I think most people know there are problems [with subwoofers], but they may not know exactly what they are, and more importantly, how to deal with them. I would like to invite you to spend more time explaining how we hear, or don't hear, 50-foot long wavelengths in a small audio control room. Perhaps discuss standing waves… just some basic stuff to let people what the problems are, and perhaps a bit about how to cope with them."
This will actually take a couple of columns. I'll start with the idea of standing waves.
LOW FREQUENCIES IN ROOMS
In case you don't recall, in my July column I wrote: "Because bass wavelengths are as large as the rooms in which we listen, their performance in such rooms varies as a function of our position in the room; and bass frequency response at any given location is more related to the room than the loudspeaker."
When the wavelength is larger than the room, it simply reflects back into the room while it is still propagating. The result is a complex set of interference patterns in the room as the propagating wave and its reflections mix together, while those reflections die away over time.
Those interference patterns do not affect the frequency of the wave, but will affect its apparent amplitude, increasing it slightly, on average, in comparison with the wave propagating in an open space where there are no reflections (called a free field).
Further, the amplitude will vary erratically as a function of both the frequency and our position in the room. Got it? Good. (Yes, I know it's confusing.)
STANDING WAVE ORIGIN
There is a special case here, which occurs when the wavelength that is propagated into the space from the loudspeaker is exactly equal to one of the room dimensions (this is particularly troublesome in rectangular rooms, which have only three such dimensions).
Assume, for example, a 22.6 Hz. wave (with a 50-foot wavelength), radiating into a room 25 feet long. That wave will propagate down the length of the room and will reflect back to the source so that exactly when the next wavefront begins to propagate from the speaker it is joined by the reflection of the first wave. (The wall boundaries are called "nodes" and the mid-point between those boundaries is called an "anti-node.")
This wave is called a "standing wave." It is called this because the nodes and antinodes of the wave are the same for the fixed room boundaries as they are for the propagating wave, so in fact, the wave appears to be stationary because all of its iterations are superimposed.
You also need to know that nodes have large variations in pressure (which is what our ears "hear") while anti-nodes have large variations in velocity (which our ears do not sense). We hear the nodes, not the anti-nodes, sort of.
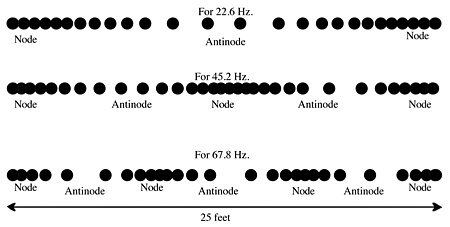
Fig. 1: Graphic showing standing nodes and antinodes for three cases (22.6 Hz., 45.2 Hz. and 67.8 Hz.) in a 25-foot room, (from “Total Recording,” courtesy of the author). Any pair of parallel walls will have a complementary resonant frequency whose wavelength is equal to twice the distance between the two walls. Further, multiples of that resonant frequency will also be resonant. Take a look at Fig. 1.
I hope this makes some sense to you, because it is important to understanding sound. At these particular frequencies, the positions of the nodes and antinodes in the room are stationary, while at all other frequencies the nodal positions vary as a function of the interference patterns that are occurring (please note that there is a lot more to this).
AUDIBLE CHARACTER
What this means is that at 22.6 Hz., if you are close to the end-wall (near node) you will hear a lot of energy, while in the middle of the room (the anti-node) you will hear almost no energy at that frequency.
Similarly, at 45.2 Hz. (2 x 22.6 Hz.), you will hear a lot of energy at the end-walls and also in the middle of the room, while you will hear almost nothing in the regions bet een the middle and the end-walls.
At 67.8 Hz. (3 x 22.6 Hz.) you will hear a lot of energy at the walls and at points one-third of the way between the end-walls, while you will hear almost nothing in the middle of the room and in the spaces between the one-third-length nodes.
The simple insight to take away from this is that there is no place in that room other than at the end-walls where you can hear all three of those frequencies at the same amplitude, i.e. with something like flat frequency response.
The standing waves are a consequence of the resonating character of the room itself!
It gets worse, actually much worse, because we have three such dimensions (length, width and height). Especially if any of those have similar dimensions, it can get really bad. In any case, each rectangular room has its own resonant frequency response and its own consequent audible frequency signature, regardless of the speaker playing into it.
WHAT DOES IT ALL MEAN?
Solving these low-frequency problems can be difficult. There are numerous approaches, including elaborate architectural solutions, extensive bass absorption, room equalization based on the response at the "listening position," room equalization based on power response, and "best fit" placement of subwoofers in the room.
And keep in mind, just solving the low-frequency room response problems may not yield the appropriate magic quality called "envelopment." Equally bad, it may yield entirely too much envelopment!
And this brings us back to the purpose of Critical Listening and control rooms: to have a stable and reliable listening situation that allows us to effectively predict how our work is going to sound in a wide variety of end-user playback environments. Next month, I'll delve into that more deeply.
Thanks for listening, and thanks, Bob!
Dave Moulton is relaxing by his pool, listening to his stereo waterfalls. You can complain to him about anything (except standing waves) at his website, www.moultonlabs.com.
