The last edition of this column talked about subnets and introduced folding paper as an illustration of how subnets can be understood. This will be very useful as we proceed.
MORE IPv4 SUBNETTING BASICS
Consider an analog clock. Start the second hand at 12:00 and follow it clockwise around the dial. At 12:00, 60 seconds have passed. Zero seconds and 60 seconds are the same place on the dial. When the second hand gets to 60, the minute hand has moved one minute. Since we keep track of time in minutes and seconds, we usually think of seconds from zero to 59, then at 60 seconds we re-set our seconds count to zero and add a minute. It’s like counting from nine to 10, where we increment the tens column when we pass nine.
It’s like that looking at IP and subnet octets. We can go from zero to 255 in each octet, but 256 means the octet is filled. We don’t have room for 256, because 255 is the limit, i.e. all binary bits are set to 1. When we hit 256, the octet changes to zero and we increment the octet to the left by one.
At home, your computer might have an IP address like 192.168.1.10. For this address, your subnet mask is probably 255.255.255.0. You decide you want two networks. Doing the mental math, you say “Two networks from one means one fold of the paper.” Each fold of the paper is a bit borrowed from the host address field. Here, you borrow one bit. That means you need to change your subnet mask. Here’s how that works:
You started off with 255.255.255.0. In binary, that’s all ones in the first three octets. To borrow, you need the first bit in the fourth octet. Here’s how it works:
11111111.11111111.11111111.00000000 is 255.255.255.0. This is where you start. You borrow the first bit in the fourth octet. The new subnet mask is 11111111.11111111.11111111.10000000.
Borrowing Table 9 from an earlier article and revising it to show the borrowing, here’s the new fourth octet:
The first bit in the fourth octet has a decimal weight of 128, so the final octet of the new subnet mask changes to 128 in decimal notation. The new subnet mask is 255.255.255.128. The way the computer sees it, this is 11111111.1111111.1111111.10000000. Since the fourth octet is where the edge of the subnet is defined, it is the critical octet here.
Hint: It is valuable to know the correlation of decimal weights (DW) of eight bit binary numbers with subnet masks (SM) values. To do this, let’s look at another table.
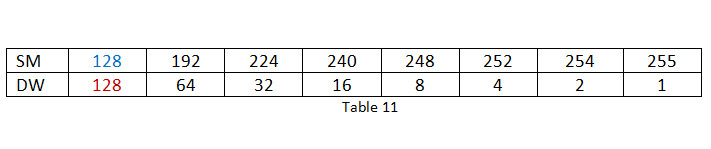
This is a good table to memorize, or to be able to regenerate at will. The SM row shows the succession of subnet mask numbers as each bit is turned on. In subnetting, we’ll be using this table a lot.
Now that we have two subnets, we have to know where each subnet starts and ends. The increment dividing one subnet from the other is the Decimal Weight from Table 11 associated with the subnet mask. In this case, note that with the subnet mask (SM) being 128, the Decimal Weight (DW) is also 128. This is also the increment between the subnets.
We know the first address in the first subnet is 192.168.1.0. This is the network IP for the first subnet. Let’s write that down as the first “Net IP.” Adding the increment, we get 192.168.1.128, the starting address of the second subnet. Next, we need the “Local Broadcast Address” for the 192.168.1.0 network. The largest number we can use without stepping on the 192.168.1.128 space is 192.168.1.127. This is the Local Broadcast Address, or LBA. For the 192.168.1.128 network, the LBA will be the largest number we can use without stepping outside the original network space. We’ll write down 192.168.1.255, meaning all bits in the fourth octet are full.
Now, we can do the math to find the available addresses in each subnet. These range from one higher than the Net IP to one less than the LBA, so we write them down in the middle column. Think of the Net IP and the LBA as the cookies and the Valid IP Addresses as the filling.
The valid IP addresses may be assigned to nodes in the network.
